Question

Heights for teenage boys and girls were calculated. The mean height for the sample of 46 boys was 195 cm and the variance was 58. For the sample of 66 girls, the mean was 165 cm and the variance was 75. Estimate how much taller teenage boys are using a 85% confidence level. Round answers to the nearest hundredth and provide the point estimate together with the margin of error.

Answer 1

With a 85% confidence level you'd expect the teenage boys to be on average between [29.217; 30.783]cm taller than the girls.

Explanation:

Hello!

Given the variables:

X₁: height of a teenage boy.

n₁= 46

`\frac{}{X}`₁= 195cm

S₁²= 58cm²

X₂= height of a teenage girl

n₂= 66

`\frac{}{X}`₂= 165cm

S₂²= 75cm²

If the boys are taller than the girls then you'd expect μ₁ > μ₂ or expressed as a difference between the two population means: μ₁ - μ₂ > 0

To estimate the difference between both populations you have to calculate the following interval:

(
`\frac{}{X}`₁-
`\frac{}{X}`₂) +
`t_(n_1+n_2-2; 1-\alpha /2)` *
`\sqrt{(S_1)/(n_1) +(S_2)/(n_2) }`

`t_(n_1+n_2-2; 1-\alpha /2)= t_(110; 0.925)= 1.450`

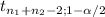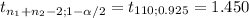
Point estimate: (
`\frac{}{X}`₁-
`\frac{}{X}`₂) = (195-165)= 30

Margin of error:
`t_(n_1+n_2-2; 1-\alpha /2)` *
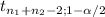`\sqrt{(S_1)/(n_1) +(S_2)/(n_2) }`= 1.450*0.54= 0.783

30 ± 0.783

[29.217; 30.783]

With a 85% confidence level you'd expect the teenage boys to be on average between [29.217; 30.783]cm taller than the girls.

I hope this helps!