Question

A person standing close to the edge on top of a 96-foot building throws a ball vertically upward. The quadratic function (t) - - 161+ 804 + 96 models the ball's height about the ground, A(t), in feet, e

seconds after it was thrown.
a) What is the maximum height of the ball?
Preview
feet
b) How many seconds does it take until the ball hits the ground?
Preview
seconds

Answer 1

196 ft

6 seconds

Explanation:

Solution:-

We have a quadratic time dependent model of the ball trajectory which is thrown from the top of a 96-foot building as follows:

`y(t) = -16t^2 + 80t + 96`

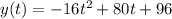
The height of the ball is modeled by the distance y ( t ) which changes with time ( t ) following a parabolic trajectory. To determine the maximum height of the ball we will utilize the concepts from " parabolas ".

The vertex of a parabola of the form ( given below ) is defined as:

`f ( t ) = at^2 + bt + c`

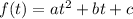
Vertex:
`t = (-b)/(2a)`

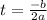
- The modelling constants are: a = -16 , b = 80.

`t = (-80)/(-32) = 2.5 s`

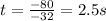
- Now evaluate the given function " y ( t ) " for the vertex coordinate t = 2.5 s. As follows:

`y ( 2.5 ) = -16 ( 2.5 )^2 + 80*(2.5) + 96\\\\y ( 2.5 ) = 196 ft\\`

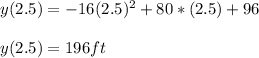
Answer: The maximum height of the ball is 196 ft at t = 2.5 seconds.

- The amount of time taken by the ball to hit the ground can be determined by solving the given quadratic function of ball's height ( y ( t ) ) for the reference ground value "0". We can express the quadratic equation as follows:

`y ( t ) = -16t^2 + 80t + 96 = 0\\\\-16t^2 + 80t + 96 = 0`

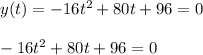
Use the quadratic formula and solve for time ( t ) as follows:

`t = (-b +/- √(b^2 - 4 ac) )/(2a) \\\\t = (-80 +/- √(80^2 - 4 (-16)(96)) )/(-32) \\\\t = (-80 +/- 112 )/(-32) = 2.5 +/- (-3.5 )\\\\t = -1, 6`

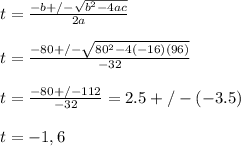
Answer: The value of t = -1 is ignored because it lies outside the domain. The ball hits the ground at time t = 6 seconds.