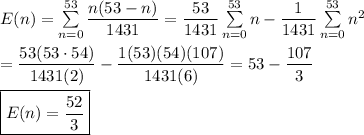Question

Two jokers are added to a $52$ card deck and the entire stack of $54$ cards is shuffled randomly. What is the expected number of cards that will be strictly between the two jokers?

Answer 1

52/3.

Explanation:

There are (54·53)/2 = 1431 ways the 2 jokers can be placed in the 54-card deck. We can consider those to see how the number of cards between them might work out.

Suppose we let J represent a joker, and - represent any other card. The numbers of interest can be found as follows:

For jokers: JJ---... there are 0 cards between. This will be the case also for ...

-JJ---...

--JJ---...

and so on, down to ...

...---JJ

The first of these adjacent jokers can be in any of 53 positions. So, the probability of 0 cards between is 53/1431.

__

For jokers: J-J---..., there is 1 card between. The first of these jokers can be in any of 52 positions, so the probability of 1 card between is 52/1431.

__

Continuing in like fashion, we find the probability of n cards between is (53-n)/1431. So, the expected number of cards between is ...

`E(n)=\sum\limits_(n=0)^(53){(n(53-n))/(1431)}=(53)/(1431)\sum\limits_(n=0)^(53){n}-(1)/(1431)\sum\limits_(n=0)^(53){n^2}\\\\=(53(53\cdot 54))/(1431(2))-(1(53)(54)(107))/(1431(6))=53-(107)/(3)\\\\\boxed{E(n)=(52)/(3)}`