Question

Need help with trig questions

Answer 1

-8 i + 19 j , 105.07°

Explanation:

Solution:

- Define two unit vectors ( i and j ) along x-axis and y-axis respectively.

- To draw vectors ( v and w ). We will move along x and y axes corresponding to the magnitudes of unit vectors ( i and j ) relative to the origin.

Vector: v = 2i + 5j

• Mark a dot or cross at the origin
• Move along x-axis by 2 units to the right ( 2i )
• Move along y-axis by 5 units up ( 5j )
• Mark the point.
• Connect the origin with the marked point determined above
• Make an arrow-head at the determined point
• Lies in first quadrant

Vector: w = 4i - 3j

• Mark a dot or cross at the origin
• Move along x-axis by 4 units to the right ( 4i )
• Move along y-axis by 3 units down ( -3j )
• Mark the point.
• Connect the origin with the marked point determined above
• Make an arrow-head at the determined point
• Lies in 4th quadrant

- The algebraic manipulation of complex numbers is done by performing operations on the like unit vectors.

`2*v - 3*w = 2* ( 2i + 5j ) - 3*(4i - 3j )\\\\2*v - 3*w = ( 4i + 10j ) + ( -12i + 9j )\\\\2*v - 3*w = ( 4 - 12 ) i + ( 10 + 9 ) j\\\\2*v - 3*w = ( -8 ) i + ( 19 ) j\\`

- To determine the angle ( θ ) between two vectors ( v and w ). We will use the " dot product" formulation as follows:

v . w = | v | * | w | * cos ( θ )

v . w = < 2 , 5 > . < 4 , -3 > = 8 - 15 = -7

`| v | = √(2^2 + 5^2) = √(29) \\\\| w | = √(4^2 + 3^2) = 5\\\\`

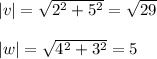
- Plug the respective values into the dot-product formulation:

cos ( θ ) =
`(-7)/(5√(29) )`

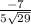
θ = 105.07°