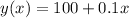Question

Simba Travel Agency arranges trips for climbing Mount Kilimanjaro. For each trip, they charge an initial fee of $100 in addition to a constant fee for each vertical meter climbed. For instance, the total fee for climbing to the Shira Volcanic Cone, which is 3000 meters above the base of the mountain, is $400.Let y represent the total fee (in dollars) of a trip where they climbed x vertical meters.Complete the equation for the relationship between the total fee and vertical distance.

Answer 1

`y(x)=100+0.1x`

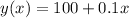
Explanation:

Let y represent the total fee (in dollars) of a trip where they climbed x vertical meters.

We know that there is an initial fee of $100, so we know that if we climb x=0 meters, we have a fee of y(0)=100.

`y(0)=100`

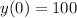
As there is a constant fee (lets called it m) for each vertical meter climbed, we have a linear relationship as:

`y(x)-y(0)=m(x-0)\\\\\\y(x)-100=mx\\\\\\y(x)=100+mx`

We know that for x=3000, we have a fee of $400, so if we replace this in the linear equation, we have:

`y(3000)=100+m(3000)=400\\\\\\100+3000m=400\\\\3000m=400-100=300\\\\m=300/3000=0.1`

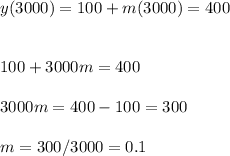
Then, we have the equation for the total fee in function of the vertical distance:

`y(x)=100+0.1x`