Question

2) The volume of water in swimming pools in a local neighborhood are normally distributed. What is the percentage of

volumes that are within 3 standard deviation of the mean?

Answer 1

The percentage of volumes that are within 3 standard deviation of the mean is 99.73%.

Explanation:

We want to calculate the area under the curve within 3 standard deviations from the mean.

If we use the standard normal distribution, this probability can be calculated as the diference between P(z<3) and P(z<-3).

`P(-3<X<3)=P(z<3)-P(z<-3)\\\\P(-3<X<3)=0.9987-0.0013=0.9973`

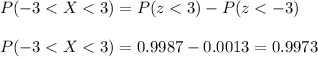
The area under the curve for the standard distribution and for any normal distribution within 3 standard deviation from the mean is 0.9973.

The percentage of volumes that are within 3 standard deviation of the mean is 99.73%.