Answer:
The values of x = 8 and x = -3 are the x-intercepts of this equation. The width of the archway is 11 units.
Explanation:
Let be
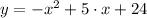 , which is now graphed with the help of a graphing tool, the outcome is included below as attachment. The values of x = 8 and x = -3 are the x-intercepts of this equation, that is, values of x such that y is equal to zero. Algebraically speaking, both are roots of the second-order polynomial.
, which is now graphed with the help of a graphing tool, the outcome is included below as attachment. The values of x = 8 and x = -3 are the x-intercepts of this equation, that is, values of x such that y is equal to zero. Algebraically speaking, both are roots of the second-order polynomial.
The width of the archway (
 ) is the distance between both intercepts, which is obtained by the following calculation:
) is the distance between both intercepts, which is obtained by the following calculation:
 , where
, where
 .
.
If
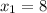 and
and
 , then:
, then:
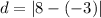

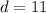
The width of the archway is 11 units.