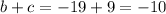Question

The roots of x^2 + 5x + 3 = 0 are p and q, and the roots of x^2 + bx + c = 0are p^2 and q^2. Find b + c.

Answer 1

b + c = -10

Explanation:

Notice that according to he quadratic formula, the solutions to a quadratic equation of the form:

`x^2+bx+c=0`

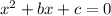
are:

`x=(-b+/-√(b^2-4\,c) )/(2)`

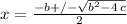
and such solutions verify the following conditions:

a) the product of the solutions is:

`((-b+√(b^2-4c) )/(2) )\,((-b-√(b^2-4c) )/(2) )=(b^2-(b^2-4c))/(4) =(4\,c)/(4) =c`

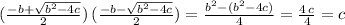
b) the addition of the solutions is:

`((-b+√(b^2-4c) )/(2) )+((-b-√(b^2-4c) )/(2) )=(-b-b)/(2) =(-2\,b)/(2) =-b`

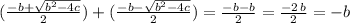
Therefore, applying these to the first equation, we get that the solutions p and q must verify:

`p\,*\,q=3\,\,\,\,and\,\,\,\,p\,+\,q=-\,5`

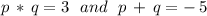
On the other hand, we know that the solutions of the equation

`x^2+bx+c=0`

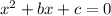
are
`p^2\,\,\, and \,\,\,q^2`

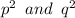
Then considering what we found in step a), the product of these two solutions should equal the constant term"c":

`p^2\,*\,q^2= c\\(p\,*\,q)\,(p\,*\,q)=c\\3\,*\,3 = c\\9=c`

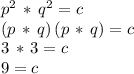
so we know the value of "c" in the second quadratic expression: c = 9

Now, according to what we found in step b), the addition of the two solutions for the second quadratic expression should equal the opposite of the coefficient in the linear term. That is:

`p^2+q^2=-b`

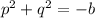
So, we need to find what the addition of these two squares is in order to find "b". We consider then what the expression
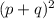`(p+q)^2` renders, since we know that
`(p+q)=-5`:

`(p+q)^2=p^2+2\,p\,q+q^2\\(-5)^2=p^2+q^2+2\,(p\,*\,q)\\25=p^2+q^2+2\,(3)\\p^2+q^2=25-6\\p^2+q^2=19`

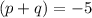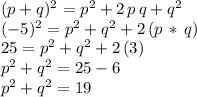
This means that

`-b=19\\\\b=-19`

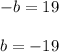
Now, knowing b and c, we can find what b+c is:

`b+c=-19+9=-10`

Answer 2

`\large \boxed{\sf \ \ \ b=-19, \ \ c=9, \ \ \ b+c=-10 }`

Explanation:

Hello,

we can write

`x^2+5x+3=(x-p)(x-q)=x^2-(p+q)x+pq`

it means that p+q = -5 and pq=3

And then we are looking for b and c so that

`x^2+bx+c=(x-p^2)(x-q^2)=x^2-(p^2+q^2)x+p^2q^2`

So

`b=-(p^2+q^2)=-[(p+q)^2-2pq]=-[(-5)^2-2*3]=-(25-6)=-19\\\\c=p^2q^2=3^2=9`

Hope this helps.

Do not hesitate if you need further explanation.

Thank you