Answer:
We get the sum of numbers rounded off to nearest 100 = 300
Explanation:
Integers from 1 to 10 inclusive.
Squaring them:
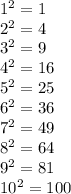
Rounding each of them to the nearest 100:
All the number less than 50 are rounded off to previous 100, which is 0.
All the other numbers i.e. 64, 81 are rounded off to 100.
100 is already rounded off, we do not need to round it off.
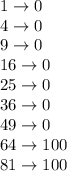
Now, taking the sum of the rounded off numbers:
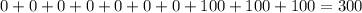
We get the sum of numbers rounded off to nearest 100 = 300
Calculating actual sum of squares from 1 to 10:
Using the formula:
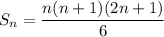
Here n = 10
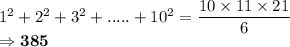
And sum of rounded off numbers = 300