Final answer:
To calculate the future value of an investment with compound interest, use the formula: A = P(1 + r/n)
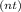 . In this case, the future value of the investment is $71,172.24.
. In this case, the future value of the investment is $71,172.24.
Step-by-step explanation:
To calculate the future value of an investment with compound interest, we can use the formula: A = P(1 + r/n)
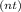 , where A is the future value, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
, where A is the future value, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
In this case, the couple deposits $21,000 with an annual interest rate of 7% for 20 years, compounded monthly. So P = $21,000, r = 0.07, n = 12, and t = 20.
Plugging these values into the formula, we get A = 21000(1 + 0.07/12)⁽¹²×²⁰⁾ = $71,172.24.
Therefore, the future value of the investment will be $71,172.24.