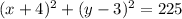Answer:
See below.
Explanation:
Let's first find the equation of the smallest circle. We know the center is at (-4,3) and the radius is 3 units. Recall the equation for a circle:

Where (h,k) is the center and r is the radius.
Plugging the numbers in, we get:
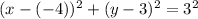
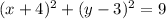
Each subsequent circle's radius is 4 units greater than the smallest circle. Importantly, note that the center will remain unchanged. The largest circle will have a radius of 3 + 4 + 4 + 4 = 15. We simply need to change the r:

Thus, equation for the fourth circle is: