Question

The two-way table shows the distribution of gender to favorite film genre for the senior class at Mt. Rose High School.

Which statement is true?
The probability of randomly selecting a student who has a favorite genre of drama and is also female is about 17 percent.
Event F for female and event D for drama are independent events.
The probability of randomly selecting a male student, given that his favorite genre is horror, is
16/40
.
Event M for male and event A for action are independent events.

Answer 1

The second statement is correct

Explanation:

Hello!

The table shows the information of the favorite film genre of the students of the class regarding their gender.

You have to prove which statement is correct:

1)The probability of randomly selecting a student who has a favorite genre of drama and is also female is about 17 percent.

If you chose a student at random, you need to calculate the probability of its favorite genre being "Drama" (D) and the student being female (F), symbolically: P(D∩F)

To do so you have to divide the number of observed students that are female and like drama by the total number of students:

P(D∩F)=
`(24)/(240)= (1)/(10) =0.10`

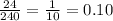
This means that the probability of choosing a student at random and it being a female that likes drama is 10%.

This statement is incorrect.

2) Event F for female and event D for drama are independent events.

Two events are independent when the occurrence of one of them doesn't affect the probability of occurrence of the other one.

So if F and D are independent then:

P(F)= P(F|D)

-or-

P(D)=P(D|F)

The probability of the event "Female" is equal to
`P(F)= (Total females in the class)/(n) = (144)/(240) = (3)/(5)= 0.6`

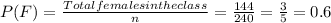
The probability of the event "Drama" is:

`P(D)= (Total students that like`

`P(F|D)= (P(FnD))/(P(D))= ((1)/(10) )/((1)/(6) )= (3)/(5) = 0.6`

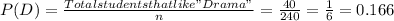
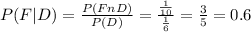
As you can see P(F)= 0.6 and P(F|D)= 0.6 so both events are independent.

This statement is correct.

3) The probability of randomly selecting a male student, given that his favorite genre is horror, is 16/40

This is a conditional probability, you already know that the student likes horror movies (H), and out of that group you want to know the probability of the student being male (M):

`P(M|H)= (number of male students that like horror movies)/(total students that like horror movies)= (16)/(38)= (8)/(19) = 0.42`

This statement is incorrect.

4) Event M for male and event A for action are independent events.

Same as the second statement, if the events "Male" and "Action" are independent then:

P(M)= P(M|A)

-or-

P(A)= P(A|M)

`P(M)= (96)/(240)= (2)/(5)= 0.4`

`P(A)= (72)/(240) =(3)/(10)= 0.3`

`P(AnM)= (28)/(240)= (7)/(60)= 0.11666`

`P(M|A)= (P(MnA))/(P(A))= ((7)/(60) )/((3)/(10) ) = (7)/(18)= 0.3888`

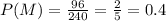
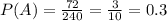
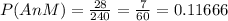
`P(M)= (2)/(5)` and
`P(M|A)= (7)/(18)`

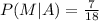
P(M)≠ P(M|A) the events are not independent.

This statement is incorrect.

I hope this helps!