Question

Olivia, a golfer, claims that her drive distance is more than 174 meters, on average. Several of her friends do not believe her, so she decides to do a hypothesis test, at a 10% significance level, to persuade them. She hits 15 drives. The mean distance of the sample drives is 188 meters. Olivia knows from experience that the standard deviation for her drive distance is 14 meters. H0: μ=174; Ha: μ>174 α=0.1 (significance level) What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?

Answer 1

3.87

Explanation:

The computation is shown below:

Data provided in the question

mean distance =
`\bar x` = 188 meters

Standard deviaton =
`\sigma = 14`

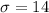
Hits drivers = 15

The distance = 174 meters

H_0: μ≤174;

H_a: μ>174

Based on the above information, the test statistic z-score is

`z = (\bar x - \mu )/(\sigma / √(n) ) \\\\ = (188 - 174)/(\ 14 / √(15) )`

= 3.87

Hence, the test statistic is 3.87

Note:

We take the μ≤174 instead of μ=174;