Question

A new city Mayor would like to determine the proportion of community voters who are ages 18 to 20 years. He has heard it is 10%. To test this prediction, he surveys 1000 random community voters and found that 111 of them are aged 18 to 20. The following is the setup for this hypothesis test: H0:p=0.10 H0:p≠0.10 The p-value for this hypothesis test is 0.04. At the 5% significance level, should he reject or fail to reject the null hypothesis?

Answer 1

Answer: He should reject the null hypothesis.

Explanation: When using P-Values to decide if you accept or not the alternative hypothesis, compare the p-value with the chosen significance level (α).

In the Mayor's survey:

p-value = 0.04

α = 5% or 0.05

If the p-value is less than α, reject the null hypothesis and accept the alternative. If p-value is greater than or equals α, fail to reject the null hypothesis and don't accept the alternative.

Analysing the Mayor's survey:

p-value = 0.04 < α = 0.05

In conclusion, the Mayor should reject the null hypothesis and accept that the proportion of voters who are aged 18 to 20 is not equal to 10%, i.e., accept the alternative hypothesis:
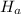`H_(a)`: p≠0.10