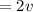Question

a tire is rolling along a road, without slipping with a velocity v. a piece of tape is attached to the tire. When the tape is opposite the road (at the top of the tire), its velocity with respect to the road is

Answer 1

The right solution will be the "2v".

Step-by-step explanation:

For something like an object underneath pure rolling the speed at any point is calculated by:

⇒
`v_(rolling)=v_(translational)+v_(rotational)`

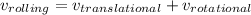
Although the angular velocity was indeed closely linked to either the transnational velocity throughout particular instance of pure rolling as:

⇒
`\omega=(v_(translational))/(r)`

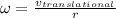
Significant meaning is obtained, as speeds are in the same direction. Therefore the speed of rotation becomes supplied by:

⇒
`v_(rotational)=\omega * r`

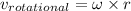
On substituting the estimated values, we get

⇒
`=(v_(translational))/(r) * r`

⇒
`=v_(translational)`

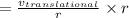
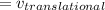
So that the velocity will be:

⇒
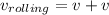
`v_(rolling)=v+v`

⇒
`=2v`