Answer and Step-by-step explanation: For an exponential distribution, the probability distribution function is:
f(x) = λ.
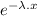
and the cumulative distribution function, which describes the probability distribution of a random variable X, is:
F(x) = 1 -
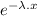
(a) Probability of distance at most 100m, with λ = 0.0143:
F(100) = 1 -
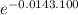
F(100) = 0.76
Probability of distance at most 200:
F(200) = 1 -
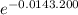
F(200) = 0.94
Probability of distance between 100 and 200:
F(100≤X≤200) = F(200) - F(100)
F(100≤X≤200) = 0.94 - 0.76
F(100≤X≤200) = 0.18
(b) The mean, E(X), of a probability distribution is calculated by:
E(X) =
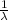
E(X) =
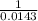
E(X) = 69.93
The standard deviation is the square root of variance,V(X), which is calculated by:
σ =
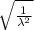
σ =
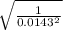
σ = 69.93
Distance exceeds the mean distance by more than 2σ:
P(X > 69.93+2.69.93) = P(X > 209.79)
P(X > 209.79) = 1 - P(X≤209.79)
P(X > 209.79) = 1 - F(209.79)
P(X > 209.79) = 1 - (1 -
 )
)
P(X > 209.79) = 0.0503
(c) Median is a point that divides the value in half. For a probability distribution:
P(X≤m) = 0.5
 = 0.5
= 0.5
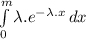 = 0.5
= 0.5
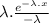 =
=
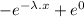
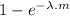 = 0.5
= 0.5
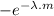 = - 0.5
= - 0.5
ln(
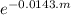 ) = ln(0.5)
) = ln(0.5)
-0.0143.m = - 0.0693
m = 48.46