Answer:
B) the particle's momentum.
Step-by-step explanation:
We know that
The centripetal force on the particle when its moving in the radius R and velocity V
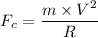
The magnetic force on the particle when the its moving with velocity V in the magnetic filed B and having charge q

At the equilibrium condition
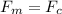
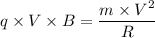
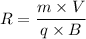
Momentum = m V
Therefore we can say that the radius of curvature is directly proportional to the particle momentum.
B) the particle's momentum.