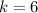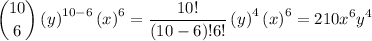Question

For the binomial expansion of (x + y)^10, the value of k in the term 210x 6y k is a) 6 b) 4 c) 5 d) 7

Answer 1

a) 6

Explanation:

Expanding the polynomial using the formula:

`$(x+y)^n=\sum_(k=0)^n \binom{n}{k} x^(n-k) y^k $`

Also

`$\binom{n}{k}=(n!)/((n-k)!k!)$`

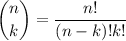
I think you mean
`210x^6y^4`

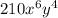
We can deduce that this term will be located somewhere in the middle. So I will calculate
`k= 5; k=6 \text{ and } k =7`.

For
`k=5`

`$\binom{10}{5} (y)^(10-5) (x)^(5)=(10!)/((10-5)! 5!)(y)^(5) (x)^(5)= (10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5! )/(5! \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 ) \\ =(30240)/(120) =252 x^(5) y^(5)$`

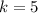
Note that we actually don't need to do all this process. There's no necessity to calculate the binomial, just
`x^(n-k) y^k`

For
`k=6`

`$\binom{10}{6} \left(y\right)^(10-6) \left(x\right)^(6)=(10!)/((10-6)! 6!)\left(y\right)^(4) \left(x\right)^(6)=210 x^(6) y^(4)$`