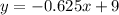Answer:
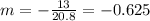
Nowe we can find the means for x and y like this:
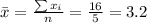
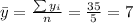
And we can find the intercept using this:

So the line would be given by:
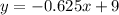
Explanation:
We have the following data:
X: 3,3,2,1,7
Y:6,7,8,9,5
We want to find an equationinf the following form:
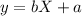
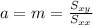
Where:

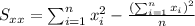
So we can find the sums like this:
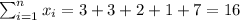
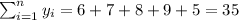
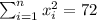
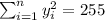
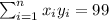
With these we can find the sums:
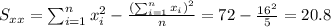

And the slope would be:
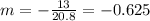
Nowe we can find the means for x and y like this:
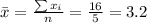
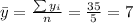
And we can find the intercept using this:

So the line would be given by: