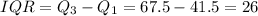Question

What is the interquartile range of the data set? {33, 38, 45, 56, 57, 63, 72, 91}

Answer 1

The correct answer is:

26

I took the test, hope this helps!

Answer 2

`IQR =Q_3 -Q_1`

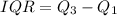
We have for this case n= 8 values. In order to find the Q1 we can select the first 4 values {33, 38, 45, 56 and the Q1 would be:

`Q_1 = (38+45)/(2)= 41.5`

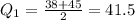
And for the Q3 we can select the last 4 values 57, 63, 72, 91 and for Q3 we got:

`Q_3= (63+72)/(2)= 67.5`

And then the interquartile range would be:

`IQR =Q_3 -Q_1 = 67.5-41.5 = 26`

Explanation:

For this problem we have the following dataset ordered:

{33, 38, 45, 56, 57, 63, 72, 91}

And we want to find the interquartile range defined as:

`IQR =Q_3 -Q_1`

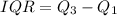
We have for this case n= 8 values. In order to find the Q1 we can select the first 4 values {33, 38, 45, 56 and the Q1 would be:

`Q_1 = (38+45)/(2)= 41.5`

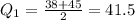
And for the Q3 we can select the last 4 values 57, 63, 72, 91 and for Q3 we got:

`Q_3= (63+72)/(2)= 67.5`

And then the interquartile range would be:

`IQR =Q_3 -Q_1 = 67.5-41.5 = 26`