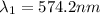Question

A non-reflective coating that has a thickness of 198 nm (n = 1.45) is deposited on top of a substrate of glass (n = 1.50). What wavelength of visible light is most strongly transmitted if it is illuminated perpendicular to its surface?

Answer 1

The wavelength is
`\lambda_ 1 = 574.2 nm`

Step-by-step explanation:

From the question we are told that

The thickness is
`t = 198 nm = 198 *10^(-9 )\ m`

The refractive index of the non-reflective coating is
`n_m = 1.45`

The refractive index of glass is
`n_g = 1.50`

Generally the condition for destructive interference is mathematically represented as

`2 * n_m * t * cos (\theta) = n * \lambda`

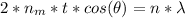
Where
`\thata`
`\theta` is the angle of refraction which is 0° when the light is strongly transmitted

and n is the order maximum interference

so

`\lambda = (2 * n * t * cos (\theta ))/(n)`

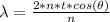
at the point n = 1

`\lambda _1 = (2 * 1.45 * 198*10^(-9) * cos (0 ))/(1)`

`\lambda_1 = 574.2 *10^(-9)`

`\lambda_1 = 574.2 nm`

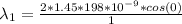
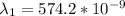
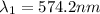
at n =2

`\lambda _2 = (\lambda _1 )/(2)`

`\lambda _2 = (574.2*10^(-9) )/(2)`

`\lambda _2 = 2.87 1 *10^(-9) \ m`

`\lambda _2 = 287. 1 nm`

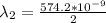
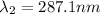
Now we know that the wavelength range of visible light is between

`390 \ nm \to 700 \ nm`

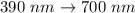
So the wavelength of visible light that is been transmitted is

`\lambda_ 1 = 574.2 nm`