Question

Solve for x: 4 over x plus 4 over quantity x squared minus 9 equals 3 over quantity x minus 3. (2 points) Select one: a. x = -4 and x = -9 b. x = 4 and x = -9 c. x = -4 and x = 9 d. x = 4 and x = 9

Answer 1

c. x = -4 or x = 9

Explanation:

`(4)/(x)+(4)/(x^2-9)=(3)/(x-3)`

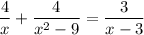
Domain:

`x\\eq0\ \wedge\ x^2-9\\eq0\ \wedge\ x-3\\eq0\\\\x\\eq0\ \wedge\ x\\eq\pm3`

solution:

`(4)/(x)+(4)/(x^2-3^2)=(3)/(x-3)`

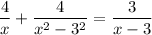
use (a - b)(a + b) = a² - b²

`(4)/(x)+(4)/((x-3)(x+3))=(3)/(x-3)`

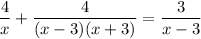
multiply both sides by (x - 3) ≠ 0

`(4(x-3))/(x)+(4(x-3))/((x-3)(x+3))=(3(x-3))/(x-3)`

cancel (x - 3)

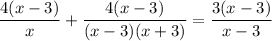
`(4(x-3))/(x)+(4)/(x+3)=3`

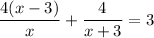
subtract
`(4(x-3))/(x)` from both sides

`(4)/(x+3)=3-(4(x-3))/(x)\\\\(4)/(x+3)=(3x)/(x)-((4)(x)+(4)(-3))/(x)\\\\(4)/(x+3)=(3x-\bigg(4x-12\bigg))/(x)\\\\(4)/(x+3)=(3x-4x-(-12))/(x)\\\\(4)/(x+3)=(-x+12)/(x)`

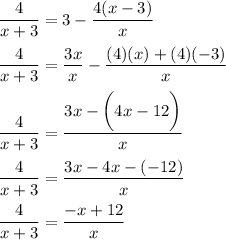
cross multiply

`(4)(x)=(x+3)(-x+12)`

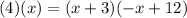
use FOIL

`4x=(x)(-x)+(x)(12)+(3)(-x)+(3)(12)\\\\4x=-x^2+12x-3x+36`

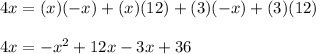
subtract 4x from both sides

`0=-x^2+12x-3x+36-4x`

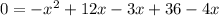
combine like terms

`0=-x^2+(12x-3x-4x)+36\\\\0=-x^2+5x+36`

change the signs

`x^2-5x-36=0\\\\x^2-9x+4x-36=0\\\\x(x-9)+4(x-9)=0\\\\(x-9)(x+4)=0`

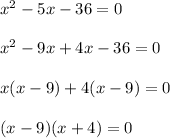
The product is 0 if one of the factors is 0. Therefore:

`x-9=0\ \vee\ x+4=0`

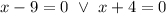
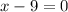`x-9=0` add 9 to both sides

`x=9\in D`

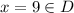
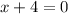`x+4=0` subtract 4 from both sides

`x=-4\in D`