Question

Find the y-intercept and the axis of symmetry of f(x)=ax2+2ax+3.

Answer 1

`y= cx^2 +dx +e`

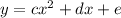
We see that:

`c = a, d= 2a , e= 3`

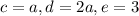
The axis of symmetry is defined by this formula:

`X= - (d)/(2c)`

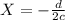
And replacing we got:

`X= -(2a)/(2a)= -1`

Thn the axis of symmetry would be X=-1

Explanation:

For this case we have the following function:

`y = ax^2 +2ax +3`

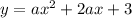
If we compare this function with the general expression of a quadratic formula given by:

`y= cx^2 +dx +e`

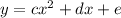
We see that:

`c = a, d= 2a , e= 3`

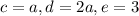
The axis of symmetry is defined by this formula:

`X= - (d)/(2c)`

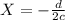
And replacing we got:

`X= -(2a)/(2a)= -1`

Thn the axis of symmetry would be X=-1