Question

Select the correct answer.

The function RX) = 2x + 3x + 5, when evaluated, gives a value of 19. What is the function's input value?
A. 1

B. -1

C. 2

D. -2

E. -3​

Answer 1

Correct option: C.

Explanation:

(Assuming the correct function is R(x) = 2x^2 + 3x + 5)

To find the input value that gives the value of R(x) = 19, we just need to use this output value (R(x) = 19) in the equation and then find the value of x:

`R(x) = 2x^2 + 3x + 5`

`19 = 2x^2 + 3x + 5`

`2x^2 + 3x -14 = 0`

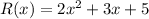
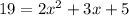
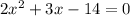
Solving this quadratic function using the Bhaskara's formula (a = 2, b = 3 and c = -14), we have:

`\Delta = b^2 - 4ac = 9 + 112 = 121`

`x_1 = (-b + √(\Delta))/2a = (-3 + 11)/4 = 2`

`x_2 = (-b - √(\Delta))/2a = (-3 - 11)/4 = -3.5`

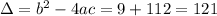
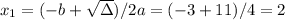
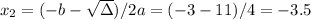
So looking at the options, the input to the function is x = 2

Correct option: C.