Answer:
Explanation:
Given that:
If C(x) = the cost of producing x units of a commodity
Then;
then the average cost per unit is c(x) =
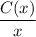
We are to consider a given function:
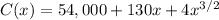
And the objectives are to determine the following:
a) the total cost at a production level of 1000 units.
So;
If C(1000) = the cost of producing 1000 units of a commodity
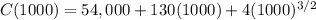
![C(1000) = 54,000 + 130000 + 4( \sqrt[2]{1000^3} )](https://img.qammunity.org/2021/formulas/mathematics/college/1ju27g6yzrinyaw5huwxnanx0rxw6excrp.png)
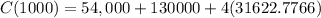

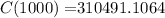
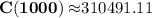
(b) Find the average cost at a production level of 1000 units.
Recall that :
the average cost per unit is c(x) =
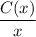
SO;
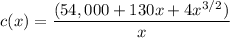
Using the law of indices
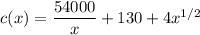
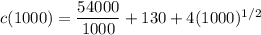
c(1000) =$ 310.49 per unit
(c) Find the marginal cost at a production level of 1000 units.
The marginal cost is C'(x)
Differentiating C(x) = 54,000 + 130x + 4x^{3/2} to get C'(x) ; we Have:
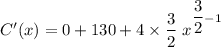

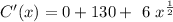

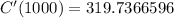
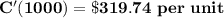
(d) Find the production level that will minimize the average cost.
the average cost per unit is c(x) =
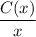
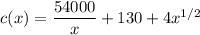
the production level that will minimize the average cost is c'(x)
differentiating
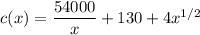 to get c'(x); we have
to get c'(x); we have

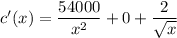
Also
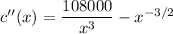
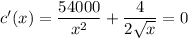
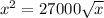
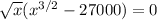
x= 0; or
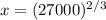 =
=
![\sqrt[3]{27000^2}](https://img.qammunity.org/2021/formulas/mathematics/college/nwd78ybn44vo8xa9rm2ofidrc8sfwf06k3.png) = 30² = 900
= 30² = 900
Since production cost can never be zero; then the production cost = 900 units
(e) What is the minimum average cost?
the minimum average cost of c(900) is
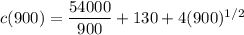
c(900) = 60 + 130 + 4(30)
c(900) = 60 +130 + 120
c(900) = $310 per unit