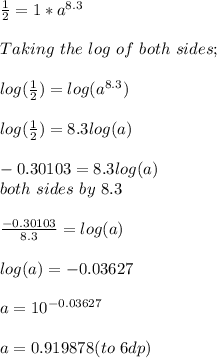Question

The half-life of iron-52 is approximately 8.3 hours. Step 1 of 3: Determine a so that A(t)=A0at describes the amount of iron-52 left after t hours, where A0 is the amount at time t=0. Round to six decimal places.

Answer 1

Explanation:

Given the half like of a material to be 8.3 hours and the amount of iron-52 left after t hours is modeled by the equation
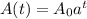`A(t) = A_0 a^(t)`, we can get A(t) as shown;

At t = 8.3 hours, A(8.3) = 1/2

Initially at t = 0; A(0) = 1

Substituting this values into the function we will have;

`(1)/(2) = 1 * a^(8.3)\\\\Taking \ the \ log \ of\ both \ sides;\\\\log((1)/(2) ) = log(a^(8.3) )\\\\log((1)/(2) ) = 8.3 log(a)\\\\\fr-0.30103 = 8.3 log(a)\\\Dividing\ both\ sides\ by \ 8.3\\\\(-0.30103)/(8.3) = log(a)\\\\log(a) = - 0.03627\\\\a =10^(-0.03627) \\\\a = 0.919878 (to\ 6dp)`