Question

A random sample of 81 observations has a mean of 20, a median of 21, a mode of 22, and a standard deviation of 3.6. The 80% confidence interval for the population mean is

Answer 1

The 80% confidence interval for the population mean is 19.48 or 20.52

Explanation:

Given that ;

the random sample size n = 81

mean
`\bar x` = 20

median = 21

mode = 22

standard deviation σ = 3.6

The 80% confidence interval for the population mean can be calculated as follows:

Firstly; the degree of freedom df = n - 1

df = 81 - 1

df = 80

At 80% confidence interval the critical value is z =
`t_(0.1, 80) = 1.292`

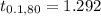
The 80% confidence interval for the population mean is =
`\bar x \pm ( z * \sigma )/(√(n))`

`= 20 \pm ( 1.292 * 3.6 )/(√(81))`

`=20 \pm ( 4.6512 )/(9)`

`= {20 \pm 0.5168 }`

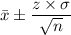
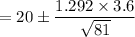
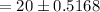
= 19.4832 or 20.5168

`\approx` 19.48 or 20.52