Question

A 3.15-kg object is moving in a plane, with its x and y coordinates given by x = 6t2 − 4 and y = 5t3 + 6, where x and y are in meters and t is in seconds. Find the magnitude of the net force acting on this object at t = 2.15 s.

Answer 1

206.67N

Step-by-step explanation:

The sum of force along both components x and y is expressed as;

`\sum Fx = ma_x \ and \ \sum Fy = ma_y`

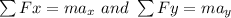
The magnitude of the net force which is also known as the resultant will be expressed as
`R =√((\sum Fx)^2 + (\sum Fx )^2)`

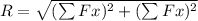
To get the resultant, we need to get the sum of the forces along each components. But first lets get the acceleration along the components first.

Given the position of the object along the x-component to be x = 6t² − 4;

`a_x = (d^2 x )/(dt^2)`

`a_x = (d)/(dt)((dx)/(dt) )\\ \\a_x = (d)/(dt)(6t^(2)-4 )\\\\a_x = (d)/(dt)(12t )\\\\a_x = 12m/s^(2)`

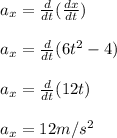
Similarly,

`a_y = (d)/(dt)((dy)/(dt) )\\ \\a_y = (d)/(dt)(5t^(3) +6 )\\\\a_y = (d)/(dt)(15t^(2) )\\\\a_y = 30t\\a_y \ at \ t= 2.15s; a_y = 30(2.15)\\a_y = 64.5m/s^2`

`\sum F_x = 3.15 * 12 = 37.8N\\\sum F_y = 3.15 * 64.5 = 203.18N`

`R = √(37.8^2+203.18^2)\\ \\R = √(1428.84+41,282.11)\\ \\R = √(42.710.95)\\ \\R = 206.67N`

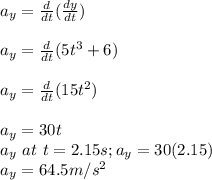
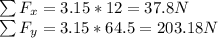
Hence, the magnitude of the net force acting on this object at t = 2.15 s is approximately 206.67N