Answer:
Part A: check B, E and F.
Part B: check E and G.
Explanation:
The equation
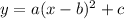 is the equation of a parabola written in the vertex form, where the vertex will be (b, c).
is the equation of a parabola written in the vertex form, where the vertex will be (b, c).
So, if the vertex is (2, -1), we have that b = 2 and c = -1
To find the c value, we use the information that the y-intercept is 3, so we have the point (0, 3). Using x = 0 and y = 3, we have:
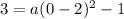
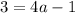
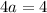
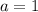
So we have a = 1, b = 2 and c = -1.
Part A: check B, E and F.
To find the x-intercepts, we need to find the values of x where y = 0:
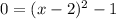
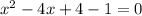

Solving using Bhaskara's formula (a = 1, b = -4 and c = 3), we have:

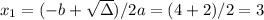
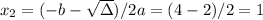
So the x-intercepts are 1 and 3
Part B: check E and G.