Question

A box of mass 0.8 kg is placed on an inclined surface that makes an angle 30 above

the horizontal, Figure 1. A constant force of 18 N is applied on the box in a direction 10°
with the horizontal causing the box to accelerate up the incline.
The coefficient of
kinetic friction between the block and the plane is 0.25.

Show the free body diagrams

(a) Calculate the block's
acceleration as it moves up the incline. (6 marks)

(b) If the block slides down at a constant speed, find the value of force applied.
(4 marks)

​

Answer 1

a) a = 17.1 m / s², b) F = 3.04 N

Step-by-step explanation:

This is an exercise of Newton's second law, in this case the selection of the reference system is very important, we have two possibilities

* a reference system with the horizontal x axis, for this selection the normal and the friction force have x and y components

* a reference system with the x axis parallel to the plane, in this case the weight and the applied force have x and y components

We are going to select the second possibility, since it is the most used in inclined plane problems, let's analyze the angle of the applied force (F) it has an angle 10º with respect to the x axis, if we rotate this axis 30º the new angle is

θ = 10 -30 = -20º

The negative sign indicates that it is in the fourth quadrant. Let's use trigonometry to find the components of the applied force

sin (-20) = F_{y} / F

cos (-20) = Fₓ / F

F_{y} = F sin (-20)

Fₓ = F cos (-20)

F_y = 18 sin (-20) = -6.16 N

Fₓ = 18 cos (-20) = 16.9 N

The decomposition of the weight is the customary

sin 30 = Wₓ / W

cos 30 = W_y / W

Wₓ = W sin 30 = mg sin 30

W_y = W cos 30 = m g cos 30

Wₓ = 0.8 9.8 sin 30 = 3.92 N

W_y = 0.8 9.8 cos 30 = 6.79 N

Notice that in the case the angle is measured with respect to the axis y perpendicular to the plane

Now we can write Newton's second law for each axis

X axis

Fₓ - fr = m a

Y Axis

N -
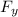`F_(y)` - Wy = 0

N =F_{y} + Wy

N = 6.16 + 6.79

They both go to the negative side of the axis and

N = 12.95 N

The friction force has the formula

fr = μ N

we substitute

Fₓ - μ N = m a

a = (Fₓ - μ N) / m

we calculate

a = (16.9 - 0.25 12.95) / 0.8

a = 17.1 m / s²

b) now the block slides down with constant speed, therefore the acceleration is zero

ask for the value of the applied force, we will suppose that with the same angle, that is, only its modulus was reduced

Newton's law for the x axis

Fₓ -fr = 0

Fₓ = fr

F cos 20 = μ N

F = μ N / cos 20

we calculate

F = 0.25 12.95 / cos 20

F = 3.04 N

this is the force applied at an angle of 10º to the horizontal