Answer:
150°
Step-by-step explanation:
Given the position of a particle in space at a time t expressed as;

Velocity of the body at t = 0 will be expressed as shown;

To get the angle between the velocity and acceleration at t = 0, we will use the formula for calculating the dot product of two vectors.
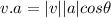
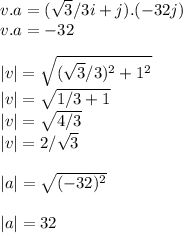
Substituting the values given into the formula, we will have;
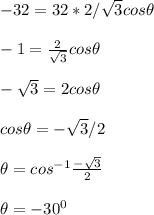
Since cos is negative in the second quadrant, the angle between the velocity and acceleration will be 180 - 30 = 150°