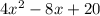Question

NEEEED HELPPPPP PLEASEEEEEE Use long division to find the quotient below.

(8x^2 + 4x^2 + 100) - (2x + 5)

Answer 1

`4x^2 - 8x + 20`

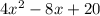
Explanation:

The correct equation is:

`8x^3 + 4x^2 + 100`

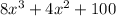
We want to divide that by (2x + 5)

To do the long division, divide each term by 2x and then subtract the product of the result and (2x + 5) from the remaining part of the equation.

When you get to 0, you have reached the end of the division.

Whatever term you get from each step of division is part of the quotient.

Go over the steps above carefully while following them below:

Step 1:

Divide
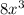`8x^3` by 2x. You get
`4x^2`.

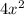Step 2

Multiply
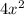`4x^2` by (2x + 5) and subtract from
`8x^3 + 4x^2 + 100`:

`8x^3 + 4x^2 + 100` - (
`8x^3 + 20x^2`) =
`-16x^2 + 100`

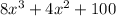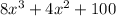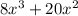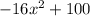
Step 3

Divide
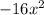`-16x^2` by 2x. You get
`-8x`.

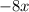Step 4

Multiply -8x by (2x + 5) and subtract from
`-16x^2 + 100`:

`-16x^2 + 100` - (
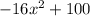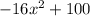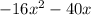`-16x^2 - 40x`) = 40x + 100

Step 5

Divide 40x by 2x. You get 20.

Step 6

Multiply 20 by (2x + 5) and subtract from 40x + 100:

40x + 100 - (40x + 100) = 0

From the three steps of the division, we got
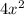`4x^2`, -8x and 20.

Therefore, the quotient is
`4x^2 - 8x + 20`