Question

Which graph represents the hyperbola x2/32-y2/82=1?

Answer 1

D

Explanation:

On edg

Answer 2

Explanation:

You have the following hyperbola:

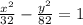`(x^2)/(32)-(y^2)/(82)=1` (1)

The general for of a hyperbola:

`(x^2)/(a^2)-(y^2)/(b^2)=1`

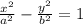
To construct the graph you take into account the rectangle formed by the lines x=±a and y=±b, and the asymptotes of the diagonals of the rectangles.

Furthermore, you take into account the foci of the hyperbola, which are

(0,±a).

Then, you have the lines

x = ± √32

y = ± √82

And the foci:

(0, ± √32)

The graph is shown in the attached image.