Answer:
The population will reach 1200 after about 2.8 years
Explanation:
The question is incomplete. Here is the complete question.
The population of a certain species of bird in a region after t years can be modeled by the function P(t) = 1620/ 1+1.15e-0.42t , where t ≥ 0. When will the population reach 1,200?
According to question we are to calculate the time t that the population P(t) will reach 1200.To do this we will substitute P(t) = 1,200 into the equation and calculate for the time 't'.
Given;
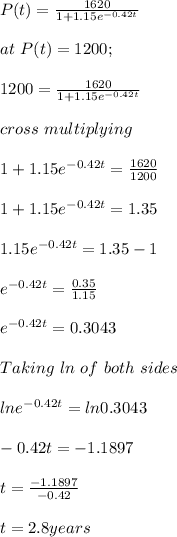
The population will reach 1200 after about 2.8 years