Answer:
No Factors
Explanation:
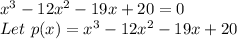
Factors of 20 = ±1, ±2 , ±4 , ±5 , ±10 and ±20
±1, ±2 and ±3 are not the factors of given polynomial.
Putting x = 4 in the given polynomial
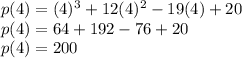
So, x = 4 is not a factor of p(x)
Putting x = -4 in the given equation
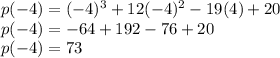
So, x = -4 in the given equation
Putting x = 5 in the given equation
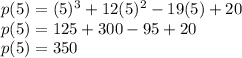
So, x = 5 is not a factor of p(x)
Putting x = -5 in the given equation
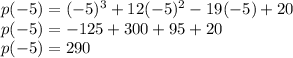
So, x = -5 is not a factor of p(x)
Putting x = 10 in the given equation
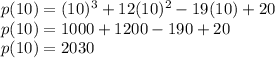
So, x = 10 is not a factor of p(x)
Putting x = -10 in the given equation
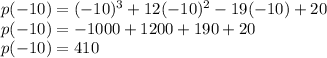
So, x = -10 is not a factor of p(x)
Putting x = 20 in the given equation
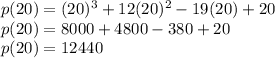
So, x = 20 is not a factor of p(x)
Putting x = -20 in the given equation
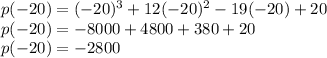
So, x = -20 is not a factor of p(x)
From the above solution, we conclude that the given equation can not be factorized and thus, has no factors.