Answer:
(See explanation below for further details).
Explanation:
Let be a parametric curve represented by
 and
and
 , where
, where
 is the parametric variable.
is the parametric variable.
The curve is represented graphically with the help of a graphing tool, whose outcome is included in the image attached below. The corresponding rectangular equation is found by eliminating t of each equation.
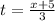 and
and
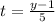
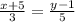
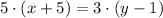

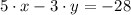
The parametric equations represents a linear function (first-order polynomial).