- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Two consecutive integers have a sum of 195. Find the integers

The integers are 97 and 98.
If integers are
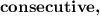 they stand right next to each other.
they stand right next to each other.
Example:- 7 and 8. 7 and 8 are consecutive integers because they stand right next to each other.
Now, let the integer be n.
The integer next to n is 1 greater than n, or n+1.
So we set up the following equation:-
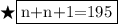
 Add the n's:-
Add the n's:-

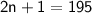
Subtract 1 on both sides:
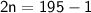
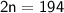
Divide by 2 on both sides:-
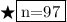
Now that we've found the first integer, finding the second integer is easy, because we can subtract the first integer from the sum of both integers:-
195-97=98
So the second integer is 98.
Quick Check:-
- 97 and 98 are consecutive
- They add up to 195:-
- 97+98=195
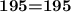
- Since the LHS (left-hand side) equals the RHS (right-hand side), the integers are indeed 97 and 98.
Good luck.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -