Question

Adult men have heights that a normally distributed with a mean of 69.5 inches and a standard deviation of 2.4 inches. Adult women have heights that a normally distributed with a mean of 63.8 inches and a standard deviation of 2.6 inches. Between a man with a height of 74 inches and a women with a height of 70 inches, who is more unusually tall within his or her respective sex ?

Answer 1

Explanation:

From the information given:

For Adult Men

Mean
`\mu` = 69.5

Standard deviation
`\sigma` = 2.4

observed value X = 74

For Adult Women

Mean
`\mu` = 63.8

Standard deviation
`\sigma` = 2.6

observed value X = 70

Therefore ; the values for their z scores can be obtained in order to determine who is more unusually tall within his or her respective sex

For Adult Men :

`z = (X- \mu)/(\sigma)`

`z = (74- 69.5)/(2.4)`

`z = (4.5)/(2.4)`

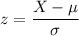
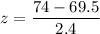
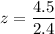
z = 1.875

For Adult Women :

`z = (X- \mu)/(\sigma)`

`z = (70- 63.8)/(2.6)`

`z = (6.2)/(2.6)`

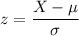
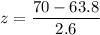
z = 2.3846

Thus; we can conclude that , the women is more unusually tall within his or her respective sex