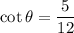Answer:
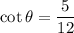
Explanation:
We are given that:
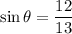
Where θ is an acute angle, and we want to find cot(θ).
Recall that sine is the ratio of the opposite side over the hypotenuse. In other words, our opposite side is measures 12 units and our hypotenuse measures 13 units.
Find the adjacent side:
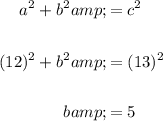
Hence, our adjacent side is 5, our opposite side is 12, and our hypotenuse is 13.
Recall that cotangent is the ratio of the adjacent side to the opposite side. Therefore:
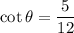
In conclusion: