Answer:
The probability is
![P[ D n R] = 0.196](https://img.qammunity.org/2021/formulas/mathematics/college/14hoegt082qfd8tczo59ovbe0ufeoklcls.png)
Explanation:
From the question we are told that
The number of Democrats is
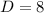
The number of republicans is
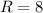
The number of ways of selecting selecting two Democrats and four Republicans.
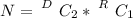
Where C represents combination
substituting values

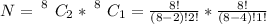
=>
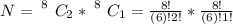
=>

=>
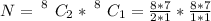
=>
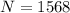
The total number of ways of selecting the committee of six people is
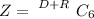
substituting values
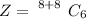

substituting values
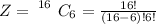
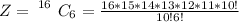


The probability of selecting two Democrats and four Republicans is mathematically represented as
![P[ D n R] = (N)/(Z)](https://img.qammunity.org/2021/formulas/mathematics/college/gq2uifksocvzcaabraqcyc07xk1fls4hhs.png)
substituting values
![P[ D n R] = (1568)/(8008)](https://img.qammunity.org/2021/formulas/mathematics/college/5vewmtbsu5cr0ws03u1dm4zhsu5jm054uh.png)
![P[ D n R] = 0.196](https://img.qammunity.org/2021/formulas/mathematics/college/14hoegt082qfd8tczo59ovbe0ufeoklcls.png)