Question

A. A hard disk has four surfaces (that's top and bottom of two platters). Each track has 2, 048 sectors and there are 131, 072 (2^17) tracks per surface. A block holds 512 bytes. The disk is not "zoned." What is the total capacity of this disk?

b. Given the disk in Part 1, how much data can be accessed without moving the disk heads. (That, is, what is the capacity of one cylinder?)

Answer 1

Step-by-step explanation:

Given that:

number of surfaces on a hard disk = 4

number of sectors = 2048 sectors

number of tracks per surface = 131, 072 (2^17)

a block holds 512 bytes.

Since, 'The disk is not "zoned.".....

then, Number of bytes / sector = 512

a) What is the total capacity of this disk?

The total capacity of the disk is:
`= 4 \ surfaces * 131072 (tracks)/(surfaces) * 2048 (sector)/(tracks) * 512 (bytes)/(sector)`

`= 5.49755814* 10^(11) \ bytes`

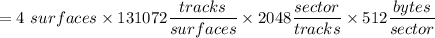
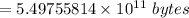
= 549755814 KB ( kilobytes)

= 549755.814 MB (megabytes)

=549.755814 GB (gigabytes)

b. Given the disk in Part 1, how much data can be accessed without moving the disk heads. (i.e what is the capacity of one cylinder?)

The capacity of one cylinder can be estimated by determining the capacity of one surface and the capacity of one track.

The capacity of one surface =
`131072(tracks)/(surface) * 2048 (sector)/(tracks) * 512(bytes)/(sector)`

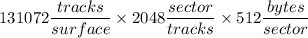
The capacity of one surface =
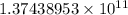`1.37438953 * 10^{11` byte = 137.44 GB

Capacity of one track = 2048 sectors/track × 512 bytes/sector

Capacity of one track = 1048576 Bytes/track

Capacity of one track =1048 KB/track

Capacity of one track ≅ 1 MB/track

Since the hard disk contains four surfaces

∴

capacity of one cylinder = 1 MB/track × 4 track/cylinder

capacity of one cylinder = 4 MB