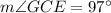Answer:
Correct answer is 4th option
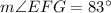 ,
,
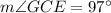
Explanation:
Given:
There are two tangents on the circle C at the point E and G.
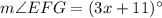 , and
, and
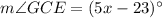
To find:
The value of central and circumscribed angles = ?
Solution:
First of all, let use recall a property of tangents on a circle.
The line joining the center of circle to the point on circle on which there is a tangent, make an angle of
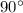 with the tangent itself.
with the tangent itself.
i.e.
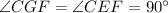 (
(
 G and F are the points on circle's tangent drawn from point F.)
G and F are the points on circle's tangent drawn from point F.)
Now, we can see that CGFE is a quadrilateral.
And sum of all internal angles of a quadrilateral is equal to
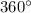
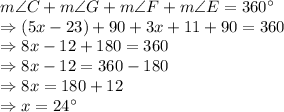
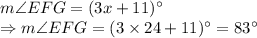
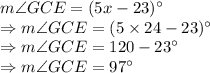
So, correct answer is 4th option
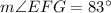 ,
,