Question

A loop of wire of area A is tipped at an angle eto uniform magnetic field B. The maximum flux occurs for an angle A=0. What angle 0 will give a flux that is of this maximum value? A. 0=30° B. 0=45 c. 0=60 d.0=90

Answer 1

We have that θ is the angle that makes the normal of the loop and the direction of the magnetic field.

This means that if θ = 0°, the plane in which the loop of wire lies is totally perpendicular to the magnetic field. (or the face of the loop points in the same direction than the field)

Now, the magnetic flux can be calculated as:

`\int\limits^} \,B.dA`

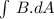
Where dA is the differential of area, and we have a dot product, then we have:

B.dA = B*Acos(θ)ds

ds is a differential of surface.

Now, the flux will be maximum when cos(θ) is also a maximum.

And the maximum of the cosine is:

Cos(0°) = 1.

decreasing until cos(90°) = 0

Now, the options given are:

30°, 45°, 60° and 90°.

Then in this range, the maximum flux will occur at the angle closer to 0°, then the correct option is θ = 30°