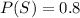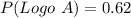Question

School administrators asked a group of students and teachers which of two

school logo ideas, logo A or logo B, they prefer. This table shows the results.
Logo A
Logo B
Total
Students
67
33
100
Teachers
11
14
25
Total
78
47
125
Are being a student and preferring logo A independent events? Why or why
not?
O A. No, they are not independent, because Astudent) = 0.8 and
A student|logo A) = 0 62.
B. No, they are not independent because P(student) = 0.8 and
A student logo A) 0.86.
C. Yes, they are independent because P(student) = 0.8 and
A student logo A) 0.86
D. Yes, they are independent, because student) = 0.8 and
A student logo A) = 0.62​

Answer 1

Answer: b

Step-by-step explanation: just took the quiz

Answer 2

The events are not independent

`P(S) = 0.8`

`P(Logo\ A) = 0.62`

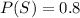
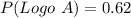
Explanation:

Given

--------------Logo A --- Logo B ---Total

Students ----- 67----------33--------100

Teachers ----- 11 ----- ----- 14 ----- 25

Total ----- ------78-----------47--------125

Required

Determine if being a student and preferring logo A are independent events

Let P(S) represent probability of being a student

Let P(Logo A) represent probability of preferring logo A

Let P(S n Logo A) represent probability of being a student and preferring logo A

To determine if they are independent, we have to calculate

P(S), P(Logo A) and P(S n Logo A)

P(S) = Total Students / Total Population

`P(S) = 100/125 = 0.8`

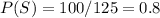
P(Logo A) = Total that prefers Logo A / Total Population

`P(Logo\ A) = 78/125 =0.624`

P(S n Logo A) = Number of students that prefer logo A / Total Population

`P(S\ n\ Logo\ A) = 67/125 = 0.536`

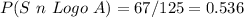
If the events are independent, then the following condition must be satisfied

`P(S\ n\ Logo\ A) = P(S) * P(Logo\ A)`

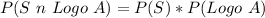
Substitute the values of P(S), P(Logo A) and P(S n Logo A)

`0.536 = 0.8 * 0.536`

`0.536 \\eq 0.4288`

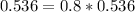
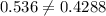
Since they are not equal, then the events are not independent

`P(S) = 0.8`

`P(Logo\ A) = 0.62`