Answer:
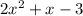
Explanation:
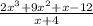
Write
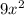 as a sum
as a sum
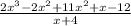
Write X as a sum
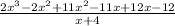
Factor out
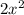 from the expression
from the expression
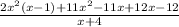
Factor out 11x from the expression
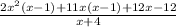
Factor out 12 from the expression
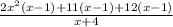
Factor out X - 1 from the expression
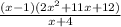
Write 11x as a sum
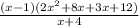
Factor out 2x from the expression
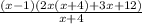
Factor out 3 from the expression
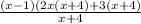
Factor out X + 4 from the expression

Reduce the fraction with X + 4
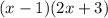
Multiply the parantheses
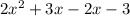
Collect like terms
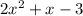
Hope this helps...
Good luck on your assignment...