Answer:
The graph is shown below.
Explanation:
The given piecewise function is
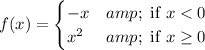
From the given piecewise function, it is clear that
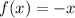 for x<0.
for x<0.
Put different values of x in f(x) where x<0 and find the values of f(x) to make a table of values as shown below.
Table of values:
x f(x)
-3 3
-2 2
-1 1
Now, plot the points (-4,4),(-3,3),(-2,2),(-1,1) and join them by straight line. There is an open circle at x=0 because 0 is not included in this function.
From the given piecewise function, it is clear that
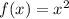 for
for
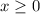 .
.
Table of values:
x f(x)
0 0
1 1
2 4
Plot the points (0,0), (1,1), (2,4) and join them by a curve. There is closed circle at 0 because 0 is included in this function.
The graph is shown below.