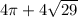Question

Find the area and the perimeter of the figure. Use in terms of pi. (no approximations)

Answer 1

See below.

Explanation:

So first, we can separate the entire figure into a semi-circle and an isosceles triangle.

AREA:

The area for a semi-circle is
`(1)/(2)\pi r^2`.

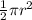The diameter is 8cm, so the radius is 4cm.

Area of the semi-circle is:

`(1)/(2)(4)^2\pi=(1)/(2)(16\pi)=8\pi cm^2`

The area for a triangle is
`(1)/(2)bh`.

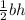The base is the same as the diameter (8), and we are given the height as 10. Thus:

`(1)/(2) (8)(10)=8(5)=40cm^2`

The total area is
`(8\pi +40 )cm^2`

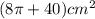
PERIMETER:

The perimeter of a semicircle is:
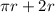`\pi r + 2r` (this is derived from dividing the circumference by 2 and then adding on the diameter).

Thus, the perimeter is:

`4\pi +8`

However, we ignore the 8 since the 8 is not part of the perimeter.

The perimeter of the triangle is the two slant lengths. We know the base and the height, so we can use the Pythagorean Theorem:

`a^2+b^2=c^2`

`4^2+10^2=c^2`

`c^2=116`

`c=√(116)=2\sqrt{29`

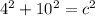
Two of them will be
`4√(29)`

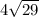
Thus, the total perimeter is
`4\pi + 4√(29)`