Answer:
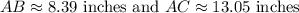
Explanation:
Note that we are given the measure of ∠C and the length of side BC.
To find AB, we can use the tangent ratio. Recall that:
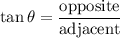
Substitute in appropriate values:
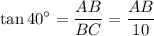
Solve for AB:
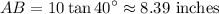
For AC, we can use cosine ratio since we have an adjacent and need to find the hypotenuse. Recall that:

Substitute in appropriate values:
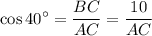
Solve for AC:
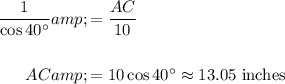
In conclusion, AB is about 8.39 inches and AC is about 13.03 inches.