Answer:
A.
Explanation:
A is incorrect. The definition of logarithms is that if
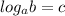 , then
, then
 .
.
The variables are in the wrong place. The correct answer should be:
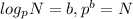
B is correct since as
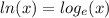 . Thus,
. Thus,
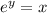
C is correct because the square root of anything is simply that thing to the one-half power.
D is also correct as this is the definition of a logarithm.