Answer: E. 10
====================================================
Explanation:
Label the friends A,B,C,D,E
There are 5 choices for the first ticket, then 4 for the second, and 3 for the third. We have 5*4*3 = 20*3 = 60 permutations. One permutation is ABC and another permutation is CBA if order mattered. However, order does not matter. All that counts is the group overall rather than the individual. This is because there is no ranking and all the friends are effectively treated equally.
With a set like {A,B,C} there are 3! = 3*2*1 = 6 ways to arrange this set of three items. This means we have overcounted by a factor of 6. Divide the previous result (60) by 6 to get 60/6 = 10
So there are exactly 10 different groups possible.
-------------
You can use the combination formula
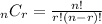
with n = 5 and r = 3 to get the same result.
Or you could use Pascal's triangle to find "10" located in the row that has 1,5,10,10,5,1. Notice how 10 is located in slot 3. You start counting at slot 0.